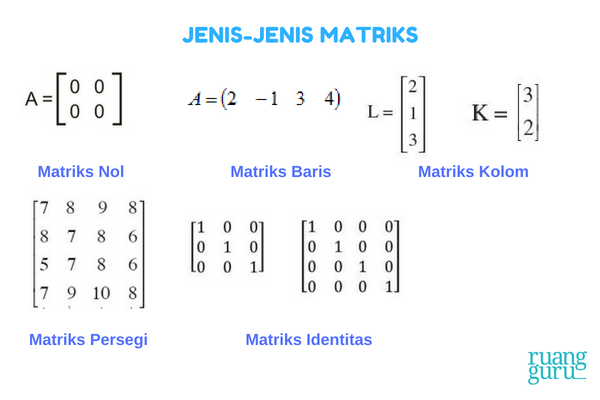
Dalam dunia matematika, matriks merupakan salah satu konsep yang sangat signifikan dan memainkan peran penting dalam berbagai cabang ilmu, mulai dari aljabar linier, statistika, hingga ilmu komputer. Kenyataan ini membuat pemahaman tentang berbagai jenis matriks menjadi esensial, terutama bagi para pelajar dan profesional yang ingin mendalami bidang-bidang tersebut. Dalam artikel ini, kita akan membahas sepuluh jenis matriks yang sering digunakan dalam dunia matematika, mengungkap karakteristik dan aplikasi masing-masing matriks.
- Matriks Persegi
Matriks persegi adalah matriks yang memiliki jumlah baris sama dengan jumlah kolom. Umumnya, matriks ini digunakan dalam berbagai aplikasi, seperti dalam sistem persamaan linier. Misalnya, matriks 2×2 atau 3×3 adalah contoh matriks persegi. Salah satu sifat penting dari matriks persegi adalah adanya determinan, yang dapat memberikan informasi tentang sifat matriks tersebut, seperti invertibilitas. - Matriks Nol
Matriks nol adalah matriks yang semua elemennya adalah nol. Jenis matriks ini berfungsi sebagai elemen identitas dalam operasi penjumlahan matriks, karena jika matriks nol dijumlahkan dengan matriks lainnya, hasilnya adalah matriks tersebut. Dalam konteks aljabar, matriks nol juga berperan dalam penelitian solusi sistem persamaan. - Matriks Identitas
Matriks identitas adalah matriks persegi yang memiliki nilai 1 di sepanjang diagonal utama dan 0 di seluruh elemen lainnya. Matriks ini berfungsi sebagai elemen identitas dalam operasi perkalian matriks, mirip dengan angka 1 dalam perkalian bilangan. Matriks identitas sangat penting dalam proses invers matriks. - Matriks Transpos
Matriks transpos diperoleh dengan mengubah baris menjadi kolom dan kolom menjadi baris. Proses ini memiliki banyak aplikasi, terutama dalam operasi matematis dan perhitungan yang melibatkan matriks. Matriks transpos sering digunakan dalam analisis data dan statistik, di mana identitas dari kelompok data harus diubah. - Matriks Simetris
Matriks simetris adalah matriks persegi di mana elemen-elemen yang berposisi simetris terhadap diagonal utama memiliki nilai yang sama. Contohnya, elemen di posisi (i,j) harus sama dengan elemen di posisi (j,i). Matriks ini sering digunakan dalam statistik dan teori graf, serta dalam berbagai aplikasi teknik. - Matriks Skew-Simetri
Matriks skew-simetri adalah matriks persegi yang memenuhi sifat bahwa elemen pada posisi (i,j) adalah negatif dari elemen pada posisi (j,i). Dengan kata lain, A[i][j] = -A[j][i]. Jenis matriks ini sering digunakan dalam mekanika dan teori kontrol, di mana sifat anti-simetri sangat relevan. - Matriks Diagonal
Matriks diagonal adalah matriks persegi yang memiliki elemen non-nol hanya di sepanjang diagonal utama dan nol di tempat lain. Contoh dari matriks diagonal adalah matriks yang memiliki skalar di diagonal utama. Matriks ini memiliki aplikasi dalam berbagai algoritma, di antaranya dalam pemecahan sistem persamaan linier dan dalam transformasi geometris. - Matriks Sparse
Matriks sparse adalah matriks yang sebagian besar elemennya nol. Jenis matriks ini biasa muncul dalam aplikasi komputasi yang melibatkan data besar, seperti di dalam pemrosesan citra dan machine learning. Penggunaan matriks sparse dapat menghemat memori dan waktu komputasi, sehingga meningkatkan efisiensi algoritma. - Matriks Ortogonal
Matriks ortogonal adalah matriks persegi yang kolom-kolomnya saling ortogonal dan memiliki norma satu. Dalam kata lain, jika A adalah matriks ortogonal, maka A^T * A = I, di mana A^T adalah transpos dari A dan I adalah matriks identitas. Dalam analisis data dan pemodelan, matriks ortogonal membantu dalam menjaga stabilitas numerik. - Matriks Hermitian
Matriks Hermitian adalah matriks persegi di mana elemen pada posisi (i,j) adalah konjugat kompleks dari elemen pada posisi (j,i). Matriks ini sangat penting dalam analisis dan aplikasi fisika kuantum, di mana sifat simetri dan konjugasi kompleks berperan dalam pemodelan sistem fisik.
Setiap jenis matriks yang telah dibahas di atas memiliki karakteristik dan aplikasi unik yang sangat berharga dalam memahami dan menyelesaikan berbagai masalah matematika. Dari matriks persegi hingga matriks Hermitian, keanekaragaman ini menunjukkan betapa kaya dan kompleksnya dunia matriks. Melalui pemahaman yang mendalam terhadap jenis-jenis matriks ini, kita tidak hanya dapat meningkatkan kemampuan analitis kita, tetapi juga membuka cakrawala baru dalam berbagai bidang, mulai dari teknik hingga ilmu sosial. Sebagai penutup, mempelajari dan menguasai matriks adalah langkah kunci dalam membangun pondasi yang kuat dalam matematika dan aplikasinya di dunia nyata.