Segitiga merupakan salah satu bentuk geometri yang paling dasar dan penting dalam dunia matematika. Dengan hanya memiliki tiga sisi, segitiga adalah landasan bagi banyak konsep dalam analisis geometris, trigonometri, dan bahkan banyak cabang lain dari ilmu pengetahuan. Dalam artikel ini, kita akan membahas 10 jenis segitiga dan contoh penggunaannya dalam matematika, memberikan wawasan lebih dalam mengenai keberagaman dan kompleksitas bentuk geometris ini.
-
Segitiga Sama Sisi
Segitiga ini memiliki ketiga sisinya yang sama panjang. Dalam penggunaan matematika, segitiga sama sisi sering kali digunakan untuk mengajarkan prinsip dasar tentang kesetaraan, terutama dalam konteks teori bilangan dan geometri. Contohnya, rumus untuk menghitung luas segitiga sama sisi dapat digunakan dalam berbagai aplikasi, dari pembuatan model arsitektur hingga desain grafis.
-
Segitiga Sama Kaki
Segitiga sama kaki memiliki dua sisi yang sama panjang. Sifat simetri dari segitiga ini memungkinkan penggunaan dalam berbagai konteks, seperti dalam arsitektur dan desain. Misalnya, konsep ketinggian dan sudut pada segitiga sama kaki sering digunakan dalam analisis struktur bangunan, di mana stabilitas menjadi hal yang sangat penting.
-
Segitiga Sembarang
Segitiga sembarang adalah segitiga yang memiliki semua sisi dan sudut berbeda. Jenis segitiga ini mencerminkan banyak situasi dalam kehidupan nyata, seperti dalam analisis data dan statistik. Contohnya, dalam menghitung varians dan deviasi standar pada data yang tidak teratur, model segitiga sembarang dapat membantu dalam visualisasi dan pemahaman distribusi data.
-
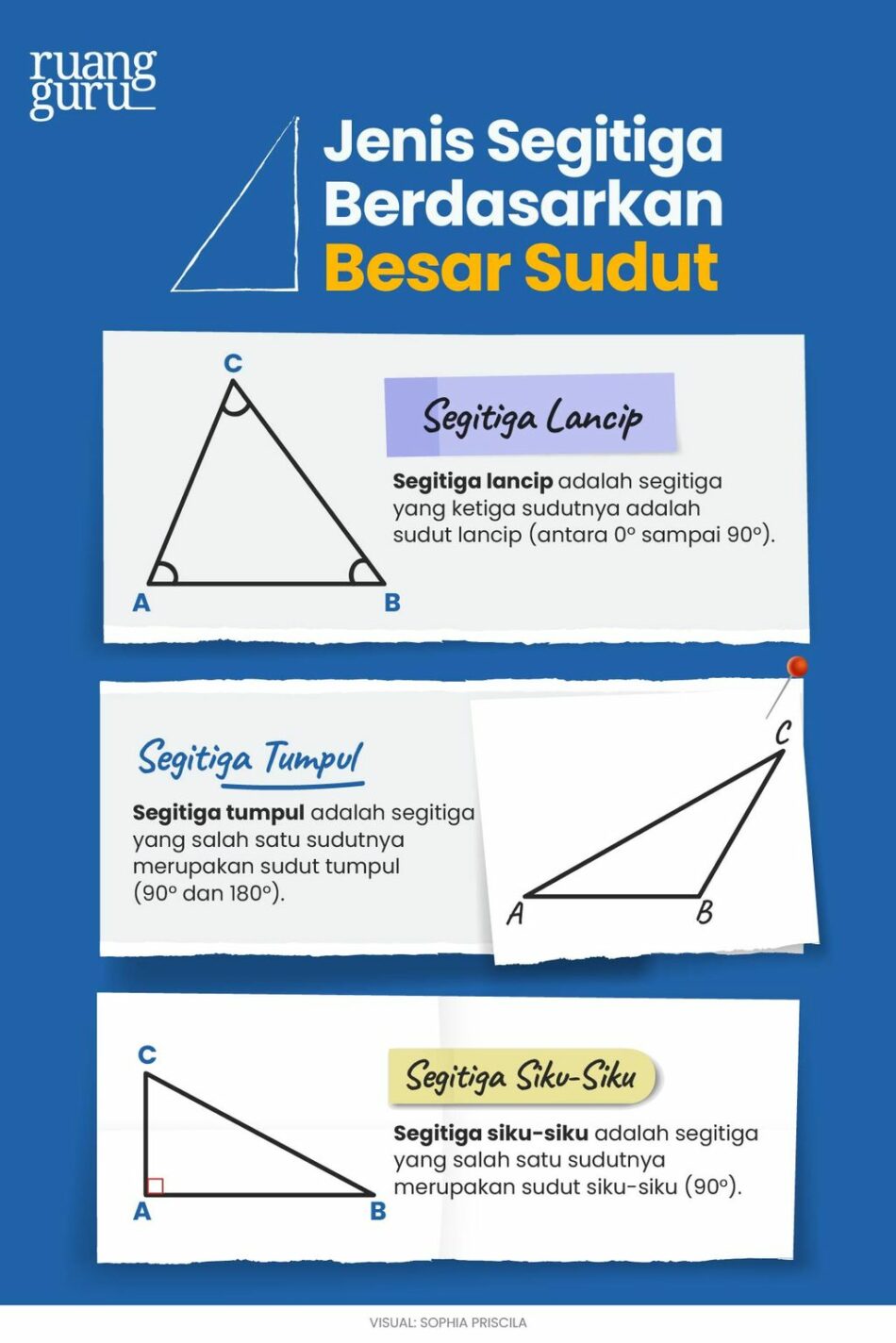
Segitiga Lancip
Segitiga lancip memiliki ketiga sudut yang kurang dari 90 derajat. Segitiga jenis ini sering digunakan dalam trigonometri untuk menentukan nilai sinus, cosinus, dan tangen dari sudut tertentu. Analisis dalam fisika dan teknik juga sering melibatkan segitiga lancip untuk memodelkan gaya dan arah.
-
Segitiga Tegak
Segitiga tegak memiliki satu sudut tepat 90 derajat. Ini adalah salah satu jenis segitiga yang paling banyak digunakan di berbagai bidang, karena banyak terkait dengan rumus Pythagoras. Dalam ilmu teknik dan arsitektur, segitiga tegak digunakan untuk menentukan ketinggian bangunan dan sudut kemiringan, serta dalam menghitung kekuatan material.
-
Segitiga Tumpul
Segitiga tumpul memiliki satu sudut lebih dari 90 derajat. Segitiga ini penting dalam banyak penerapan, termasuk dalam bidang arsitektur, di mana sudut tumpul dapat menciptakan ruang yang lebih luas. Dalam praktik, perhitungan luas segitiga tumpul membantu para arsitek memahami proporsi ruangan dalam desain.
-
Segitiga Muncul
Segitiga muncul adalah istilah yang jarang terdengar, namun umum dalam teori graf. Ini merujuk pada ketiga simpul yang terhubung dari segitiga dalam struktur data graf. Di dunia algoritma, penggunaan segitiga muncul membantu dalam memahami hubungan antar titik dalam jaringan, seperti dalam pemrograman dan analisis jaringan sosial.
-
Segitiga Isosceles Right
Segitiga ini adalah kategori khusus dari segitiga sama kaki yang memiliki satu sudut 90 derajat. Penting dalam konteks geometri dan trigonometri, segitiga ini memiliki aplikasi praktis dalam pengukuran dan konstruksi. Dalam desain dan analisis, ukuran dan proporsi segitiga isosceles right sering digunakan untuk memastikan keselarasan dan simetri perpindahan.
-
Segitiga Heronian
Segitiga Heronian adalah segitiga dengan panjang sisi yang merupakan bilangan bulat. Ini memainkan peran penting dalam teori bilangan dan geometri kombinatorial, di mana analisis bilangan bulat dapat memunculkan metode baru dalam perhitungan dan pembuktian teorema. Segitiga ini sering digunakan dalam perhitungan luas dan perbandingan struktur dalam bentuk geometris lainnya.
-
Segitiga Pitagoras
Segitiga Pitagoras adalah segitiga tegak yang panjang sisi-sisinya mematuhi hukum Pythagoras (a² + b² = c²). Konsep ini adalah dasar bagi banyak penerapan dalam matematika, fisika, dan teknik. Penggunaan rumus ini penting dalam navigasi, pengukuran jarak, serta dalam berbagai analisis geometris.
Keberagaman segitiga tidak hanya memberikan landasan yang kuat dalam memahami geometri, tetapi juga menyoroti bagaimana bentuk-bentuk ini dapat diterapkan dalam berbagai disiplin ilmu. Dari arsitektur hingga fisika, bahkan dalam bidang teknologi informasi, pemahaman yang mendalam tentang segitiga dan sifat-sifatnya membuka banyak kemungkinan penemuan dan inovasi baru. Dengan mempelajari jenis-jenis segitiga ini, kita tidak hanya mendapatkan pengetahuan teoritis tetapi juga dapat menerapkannya dalam masalah praktis yang dihadapi dalam kehidupan sehari-hari. Semoga artikel ini memberikan wawasan dan mendorong pembaca untuk lebih mengeksplorasi konsep-konsep geometri dalam matematika.