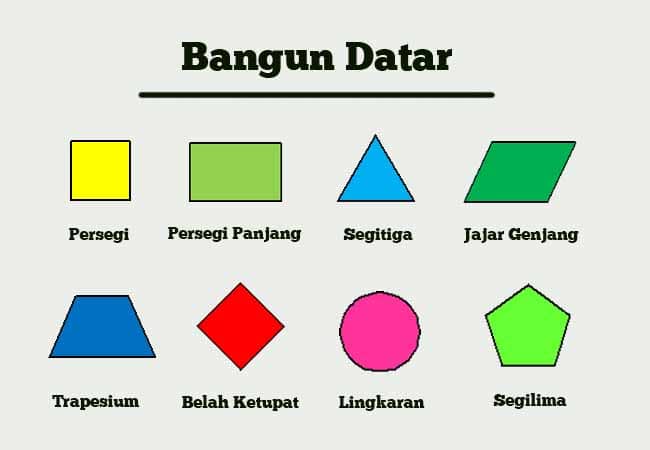
Geometri, sebagai salah satu cabang matematika, memberikan dasar penting dalam memahami bentuk dan ruang di sekitar kita. Salah satu komponen utama dalam geometri adalah bangun datar. Bangun datar adalah bentuk dua dimensi yang memiliki panjang dan lebar, tetapi tidak memiliki tinggi. Dalam artikel ini, kita akan menjelajahi sepuluh macam bangun datar yang umum ditemukan dan penting untuk dipahami. Dengan beragam jenis dan karakteristik yang dimiliki, pengetahuan tentang bangun datar ini tidak hanya berguna dalam konteks akademis, tetapi juga dalam kehidupan sehari-hari.
- Persegi: Persegi adalah bangun datar yang memiliki empat sisi yang sama panjang dan empat sudut yang siku-siku. Luas dari persegi dapat dihitung dengan rumus L = s x s, di mana s adalah panjang sisi. Persegi sering digunakan dalam desain dan konstruksi karena simetri dan kestabilannya.
- Persegi Panjang: Merupakan bangun datar yang memiliki dua pasang sisi yang sejajar dan sama panjang. Perbedaan antara persegi dan persegi panjang terletak pada panjang dan lebar yang tidak sama. Luas dari persegi panjang dihitung dengan rumus L = p x l, di mana p adalah panjang dan l adalah lebar. Bangun ini banyak digunakan dalam arsitektur dan perencanaan ruang.
- Segitiga: Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Segitiga dapat dibedakan menjadi beberapa jenis: segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang. Luas segitiga dapat dihitung dengan rumus L = 1/2 x alas x tinggi. Bangun ini juga mendasar dalam banyak aplikasi, dari seni hingga struktur teknik.
- Lingkaran: Lingkaran adalah bangun datar yang dibentuk oleh semua titik yang memiliki jarak yang sama dari titik pusat. Jari-jari lingkaran adalah jarak dari pusat ke tepi, sementara diameter adalah dua kali jari-jari. Luas lingkaran dapat dihitung dengan rumus L = π x r². Lingkaran banyak ditemukan dalam berbagai aspek, mulai dari bentuk jam hingga desain logo.
- Jajargenjang: Jajargenjang adalah bangun datar yang memiliki dua pasang sisi yang sejajar dan sama panjang, mirip dengan persegi panjang, tetapi sudutnya tidak selalu siku-siku. Luasnya dihitung dengan rumus L = alas x tinggi. Jajargenjang sering digunakan dalam desain grafis dan seni visual karena bentuknya yang dinamis.
- Trapesium: Trapesium adalah bangun datar yang memiliki sepasang sisi yang sejajar. Bentuk ini dapat dibedakan menjadi trapesium sama kaki (dengan sisi miring yang sama panjang) dan trapesium sembarang. Luas trapesium dapat dihitung dengan rumus L = 1/2 x (a + b) x t, di mana a dan b adalah panjang sisi sejajar, dan t adalah tinggi. Trapesium sering dihadirkan dalam berbagai bidang rekayasa dan arsitektur.
- Belah Ketupat: Belah ketupat adalah bangun datar yang memiliki empat sisi yang sama panjang, dengan sudut berlawanan yang sama besar. Luas dari belah ketupat dapat dihitung dengan rumus L = d1 x d2 / 2, di mana d1 dan d2 adalah panjang diagonal. Belah ketupat memiliki kekhasan visual yang sering digunakan dalam desain grafis dan seni.
- Layang-Layang: Layang-layang adalah bangun datar dengan dua pasang sisi yang berukuran sama tetapi berbeda dalam panjang. Layang-layang memiliki sifat simetris dan dapat dibedakan menjadi layang-layang biasa dan layang-layang yang memiliki sudut yang lebih besar. Luasnya dihitung dengan rumus L = d1 x d2 / 2, di mana d1 dan d2 adalah panjang diagonal. Bentuk ini sering digunakan dalam origami dan perancangan seni.
- Segi Empat: Segi empat adalah bangun datar yang memiliki empat sisi. Jenis segi empat ini termasuk persegi, persegi panjang, jajargenjang, dan trapesium. Rumus luas segi empat bervariasi tergantung pada jenisnya. Segi empat banyak digunakan dalam berbagai bidang, termasuk arsitektur dan desain produk.
- Segi Banyak: Segi banyak adalah bangun datar dengan sisi yang lebih dari tiga. Segi banyak dapat berupa segi lima, segi enam (heksagon), segi tujuh (heptagon), dan seterusnya. Luas segi banyak dapat dihitung dengan berbagai cara tergantung pada jenis dan ukuran decagon yang diinginkan. Segi banyak sering dihadapi dalam desain geometris dan arsitektur.
Pemahaman tentang bangun datar merupakan langkah awal yang penting dalam belajar geometri. Dengan mengetahui sepuluh macam bangun datar ini, kita tidak hanya dapat memahami bentuk-bentuk di sekeliling kita, tetapi juga dapat mengaplikasikannya dalam berbagai disiplin ilmu. Melalui penguasaan konsep ini, kita dapat mengembangkan pemikiran logis dan analitis yang diperlukan untuk memecahkan masalah yang lebih kompleks dalam geometri dan di luar itu.
Dengan adanya berbagai macam bangun datar ini, diharapkan pembaca dapat lebih memahami karakteristik serta penggunaan dari masing-masing bentuk. Pengetahuan ini tidak hanya bermanfaat untuk tujuan akademis, tetapi juga memperkaya pemahaman kita tentang dunia visual dan spasial di sekitar kita. Di bidang seni, arsitektur, dan teknik, pemahaman yang mendalam tentang bangun datar dapat membuka peluang untuk kreativitas serta inovasi baru.